比特派钱包下载官方app

0 引 言

浅层地表热量传输，即地表到地下十几米深度处土壤或岩石热量的传输过程.这个深度段地球介质上接大气，下接地球内部，其热量传输方面的研究对我们认识大气、地球内部及二者的热耦合有着及其重要作用.大气科学领域对其的关注比较多，如土壤温度的诊断和预报、地表能量平衡系统中土壤热通量的计算都是浅层地表热传输研究的主要内容.在固体地球物理领域，如利用浅海或湖底连续观测的沉积物温度序列获得浅海或湖底沉积物热流、以及利用变温层温度序列计算大地热流时，由于测量的深度明显浅于传统热流测试的深度(大地热流是温度梯度与热导率的乘积，传统测试大地热流时，钻井深度一般要大于300 m(Turcotte and Schubert， 2002)，求解温度梯度时都要从温度序列中去除来自于外界的高频噪音影响(汤懋苍等，1991；魏东平等，1992；Liu et al.， 2013).在求解浅海及湖底沉积物热流，需从温度序列中去除浅海水温的变化BTV(Wang and Beck， 1987；Kinoshita et al.， 1996；Hamamoto et al.， 2005).这些研究都涉及到浅层地表热传输方面知识的运用.此外，由于热导率的获取需知道热扩散率和体积热容量的大小，而热扩散率又是由序列中的高频信息结合传热模型获得，即浅地表介质热性质的获取也是浅层地表热量传输理论研究的主要内容.所以，对这部分工作进行归纳与总结具有重要意义.

浅层地表热传输研究重点是土壤温度的计算和热通量的计算，首先需要确定土壤的两个热力学参数：土壤体积热容量和土壤热传导率.土壤体积热容量是指单位体积土壤增温1℃所需要的热量，是土壤各组成成分体积热容量之和.土壤热导率是土壤传热能力大小的体现.与土壤热容量不同的是，土壤热导率虽然与土壤的组成成分及其所占比例有关，但是却不能简单地将其视为固、液、气这三相物质热导率的权重相加之和.由于这个原因，先后演化出各种不同的热导率参数化方案.在推导热传导方程的过程中，土壤热扩散率这个衍生参数随即出现了，它是指当土壤流入一定热量时，导致土壤温度升高的程度，反映土壤传导热量和消除层间温度差异的能力.许多学者在浅层土壤热传输的研究中，对如何建立浅层土壤传热模型、如何获取土壤体积热容量、热扩散率、热传导率这三个重要的参数及热通量的计算方面进行了广泛而细致的研究，并取得了大量的成果.本文在整体知识梳理的基础上，主要对比较有代表性的五类传热模型、两类典型的体积热容量计算公式、常用的四类求热扩散率的方法、五种热导率参数化方案及热通量的求解方法进行了回顾，并对各方法的主要特点及应用状况进行概述.

1 传热模型的研究概述

在研究浅层地表热量传输时，必不可少的步骤就是先建立传热模型，早期这方面的研究主要着眼于一维热传输方程的解析解，并在此基础上进一步扩展其应用.基于不同的初始及边界条件，热传输方程的解析解可由不同的方法得到.其中比较有代表性的有：传统的谐波方法(HM)、拉普拉斯变换(CLTM)、非匀质土壤方法(NHS)、双层热传导模型、水热耦合热传输的研究.不同的方法都有其优势及相应的局限性.事实上，土壤的热传输不止发生在一个方向上，近些年来，也有不少学者研究了二维热传输过程.Takakura等(1971)利用二维热传导模型模拟了室内和室外土壤的热传输过程，Kluitenberg和Horton(1990)给出了二维热传导方程的解析解.由于浅层地表热量传输主要体现在深度方向上，所以在大气科学及固体地球物理领域，大部分学者还是倾向于简化此过程为一维，即深度维，所以一维热传输方程的解析方法具有更广泛的应用价值，我们此处对几种有代表性的方法进行介绍.

1.1 只考虑热传导

考虑在z≥0区域的一个半无限空间，并假定土壤介质都遵从热传导方程.有公式

其中T为温度(℃)，z为深度变量(m)，t为时间变量(s)，κ为热扩散系数(m2/s).

(1)传统谐波法(HM)

地表温度序列T(0，t)可以写成定常温度T0上叠加了n阶随时间的周期变化部分. 公式为

其中：ωi=2π/Ti为第i阶周期变化的圆频率(rad/s)，Ti为第i阶分量的周期(s)，如一年或一天；Ai为第i阶周期变化的振幅(℃)；φi为第i阶周期变化的位相(rad).结合T(∞，t)=T0条件，利用分离变量法求解(1.1)式可得(Carslaw et al.， 1959；Van Wijk，1963)

此方法的特点是边界条件为多个谐波的叠加，由于地表温度变化中除了较明显的年周期变化外，还有其他周期分量，由小到大依次是：高频变化(时间尺度小于2天)、天气尺度变化(时间尺度为2.5~6天)、准两周、30~50天、准半年、准9个月、准两年及大气的年代际变化等.所以，以定常温度的基础上叠加多个谐波变化为边界条件能基本反映地表温度变化的真实情况，并且由此得到的解析解形式简单，计算方便.Liu等(2013)将长时间气象地温观测序列用于求解区域地表热流时用此模型模拟了浅层地表传热过程.Kinoshita等(1996)与Hamamoto等(2005)利用浅海及湖底沉积物温度序列获取沉积物热流时也用此模型模拟了沉积物的温度变化，近而从温度序列中去除BTV的影响.由此模型的解析解(1.3)式还可推导出几个常用的热扩散系数的计算方法，本文的下部分将进行具体介绍.

(2)拉普拉斯变换(CLTM)

初始和边界条件：

利用拉普拉斯变换法求解(1.1)式可得(Carslaw et al，1959)：

此解析方法的边界条件是时间t的函数，对其形式并无限制，所以HM法的边界条件是此边界条件的一个特例.由于受初始条件是定值的限制，de Silans(1986，1988)、Balabanis(1987)在此基础上进行了改进，将初始条件改进为

进而得到改进后此模型的解析解为

其中，F(z)=Tz0+f(z)，存在深度z0，当z≥z0时，T恒定且为Tz0，即当z≥z0时f(z)=0.由于边界条件为时间的任意形式的函数，这其中包括传统谐波法中谐波形式的边界条件.当发生非周期变化时，此模型的边界条件更贴近于真实的土壤热传导过程，但在计算上有一定的复杂性，用此模型求解土壤热扩散系数时，一般由计算得到的土壤温度和实际观测得到的土壤温度最小二乘法拟合得到.

(3)非匀质土壤方法(NHS)

以上两种方法都是在土壤热性质随深度是同性的假设下推导得到，Lettau(1954)、Lettau(1971)、Nassar和Horton(1989)以稳定周期为边界条件(式(1.9)、式(1.10))，不同深度层不同热扩散系数的假设下改进了土壤热传输理论，提出了NHS方法.

其中A(z)、B(z)分别为谐波振幅，φ(z)、β(z)为谐波位相，G(z，t)是地表土壤热通量(W/m2)，由于λ=Cpκ，(1.1)式可化为

以上边界条件带入(1.11)式可得

其中，.由(1.12)可以看出热扩散系数κ是z的函数.NHS法虽然把土壤分为多层，并得到不同深度热扩散系数的计算方法，但并未给出热传输方程的解析解.从边界条件看，地表温度与地表土壤热通量是稳定温度或热通量场上叠加一个谐波，如果序列时间跨度是几天，则这一个谐波的周期是一天，如果序列的时间跨度大于一年，则这个谐波的周期是一年.虽然边界条件捕捉到了主要的周期变化，表示真实土壤的其他周期变化在此处忽略了，对计算结果是有一定的影响.

(4)双层热传导模型

魏东平等(1992)以地表温度为余弦函数形式变化为边界条件：

建立双层模型，上层深度为H，在深度H处，上下两层土壤温度满足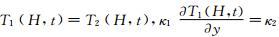：，并令∂T2(H，t)在H为无穷大时有限，其中T1、κ1是上层土壤温度及热扩散系数，T2、κ2是下层土壤温度及热扩散系数.用分离变量法解(1.1)式，可分别得出T1(y，t)、T2(y，t)的解析表达式.魏东平等(1992)在此模型的基础上，利用怀来气象站15年的深层气象地温数据，模拟了两层土壤温度的变化，并得到了怀来站附近的大地热流值为56.1 mW/m2，此热流结果与钻孔测得的当地大地热流值符合得很好.

双层热传导模型的上层边界条件假设地表土壤温度信号为一个周期谐波，而忽略了其它次要周期分量的谐波，这与实际土壤情况有一些差别.虽然模型推导过程复杂，但此模型不止能反演出两层土壤介质的热扩散系数，深度H及上下两层介质的体积热容量之比f也可得到.所以此模型和确定的物理量有4个：κ1、κ2、H、f.由于此模型的推导假设是线性的，即：y深度处土壤温度信号是与地表土壤温度信号周期相同的谐波，但振幅和位相有了相应的变化，每一层的振幅和位相的表达式都包含κ1、κ2、H、f，所以要确定这四个未知数，需知道两层或两层以上的土壤温度序列.

1.2 热传导-对流方法

以上四种方法都是在只考虑热传导过程的基础上得到.近些年来，研究表明：土壤，特别是浅层土壤的热传输过程不止有传导过程，对流过程也起着很重要的作用.综合热传导及热对流的共同作用，比特派钱包app官方下载即为耦合热传导-对流传输理论.早期， 比特派钱包官方下载此方面大量的研究工作主要集中于用数值方法模拟(Horton and Chung， 1991；Nassar and Horton， 1992a、1992b；Healy and Ronan， 1996；Koo and Kim， 2008)，解析的方法较少.综合考虑土壤热传导对流过程的解析法最早由范新岗和汤懋苍(1994)提出，Shao等(1998)在热传导-对流方程中考虑了土壤液态水通量密度的日变化求出其解析解，并利用解析方法模拟土壤渗透实验的温度资料，模拟的效果很好.Gao等(2003)认为昼夜温度及太阳辐射的差异会引发土壤水的垂直运动，此过程影响着土壤的温度分布，为了考虑这部分影响，他们开创性地建立了土壤热传导-对流模型，公式为

式(1.13)右边第二项是由于液态水垂直运动引起的能量净输入，其中，可理解为液态水通量密度(m/s)(Gao et al.， 2003)，Cg为土壤体积热容量，Cw为液态水体积热容量，w为水的垂直运动速度，θ是土壤含水量.

边界条件为定常温度场上叠加一个正弦波：

式(1.13)的解析解为

Gao等(2007a)利用在沙漠中观测到的浅层土壤温度数据对液态水通量密度W进行了细致的研究，结果表明：W普遍比热扩散系数κ大一个数量级，且随着深度的增加W有明显的减小趋势.这是由于地表水蒸发引起明显的水分渗透运动，而这种渗透作用对深层土壤的影响并不大.此外，Gao(2005)、Gao等(2007b)、王琳琳等(2008)分别将不同的野外实验数据，利用上述热传导-对流方程的解析方法进行土壤温度模拟，他们的研究认为浅层土壤，特别是水分含量丰富的裸土和稀疏植被地表，土壤水分垂直运动及土壤的深度向的不均匀性在土壤热传输模拟中的影响不容忽视.由于此解析方法的边界条件只考虑了一个正弦波，即只考虑了地表温度的日变化，王琳琳(2010)改进边界条件为一组正弦波，再结合初始条件进一步得出了热传导-对流土壤温度的预报方程.

以上五种方法可以说各有长短，除了CLTM方法，其它四种方法需要稳定周期变化的假设，如遇到突发性天气、一次强降水或寒潮天气过程，而引起的稳定周期变化的假设失效时，以稳定周期变化为边界条件的模型在模拟温度场及获取热扩散系数时误差将增大，此时CLTM方法可行. de Silans等(1996)利用两组HAPEX-Sahel实验温度数据验证得出：如果在垂直方向上热力性质不满足同性，则HM和CLTM都会高估土壤总体热扩散率，此时NHS更适合.此外，双层热传导模型还可以反演出上下两层土壤热容量之间的比值f，而土壤热容量几乎只与土壤质地有关，是个很难用土壤温度来拟合的量，当只测量了浅层土壤的质地等参数，可通过双层热传导模型可得到深层的土壤热容量，为研究提供了极大的方便.

2 热扩散率

正如前文所说，土壤热扩散率是个衍生参数，它反映土壤消除层间温度差异的能力.而实际上土壤热传导和热对流同时影响土壤温度的变化，而这必须由一个参数来说明，所以，由只考虑热传导模式下描述土壤温度变化的热扩散率的意义就需要扩展，因此，用总体热扩散率(apparent thermal diffusivity)(Horton et al.， 1983)命名此参数更为准确.由于用语习惯，本文将总体热扩散率简称为热扩散率.早期获取土壤热扩散率的途径是找出土壤热扩散率以土壤深度为变量的经验函数(Lettau，1971)，由于不同冠层覆盖及不同质地的土壤，需不同的公式，还需要连续观测不同深度的土壤温度，所以此类方法的可移植性不强.土壤热扩散率还可以实验测定(Stephenson，1987；Bristow et al.， 1994；Kluitenberg et al.， 1995；李毅和邵明安，2005)，实验取样只能取很小的部分，一个样品只能反映采样时刻的土壤状态，此法是土壤物理领域专门研究土壤热性质的学者们常用的方法，在大气科学及固体地球物理领域，应用性不是很强.此外，一些研究者着眼于有限差分方法求解热扩散率(Richtmeyer and Morton， 1967；Hinkel et al.， 1990；Gerald and Wheatley， 1989；Steele-Dunne et al.， 2010；李毅等，2003).Horton等(1983)指出在高采样频率的条件下，此方法对中间层热扩散系数的模拟精确度较高，且需三层土壤温度的观测数据.Zhang和Osterkamp(1995)将数值方法扩展到对冻土层热扩散率的计算，此外他们还对两种数值算法进行了模拟对比，发现计算结果中有奇异点现象存在.所以综合以上考虑，大家常用的做法是借助观测得到的温度序列及土壤热传输方程的解析解推求热扩散系数，此法的好处是可以得到研究时间段土壤的综合状态.并且土壤传热模型的解析方法很大程度上都是为了能够求出土壤热扩散率而做的努力.

2.1 振幅法与位相法

Horton等(1983)在HM解析方法的基础上得出了求解热扩散系数的两种常用方法，这两种方法分别由两层温度序列中主要谐波分量的振幅和位相得到：

式(2.1)为振幅法，(2.2)为位相法.其中A1、A2分别是深度z1、z2温度序列中的主要谐波分量的振幅，δt是主要谐波分量的位相差.这两个方法都是从HM方法的解析解推导得到，并进行了简化，只考虑了每层的主要谐波分量.董文杰与汤懋苍(1992)用气象地温资料计算平均土壤热流时采用了振幅法来获取台站附近土壤热扩散率，进而得到大地热流，并得出在绝大多数地区，地表热流与深层大地热流的方向和量级都一致的结论.

2.2 反正切法与对数法

接近地表土壤的温度变化可表示为定常温度场的基础上叠加一系列正弦波的形式为

将某一深度温度序列的观测值用上式进行线性最小二乘法拟合，其中T 为温度序列时间上的平均值，M为谐波数，An、Bn为不同谐波的振幅，如果只选取上式谐波分量的前4项(M=2)，Nerpin与Chudnovskiiv(1967)由此得出了热扩散系数的反正切法计算公式为

这里Tn、T′ n分别为深度z1、z2 每隔6 h观测的土壤温度(n=1，4)，Seeman(1979)在反正切法假设的基础上推导出了热扩散系数的对数法计算公式为

这两个公式是在早期无自动温度记录设备时发展出的热扩散系数计算方法，而正是由于这个原因，间隔6个小时的温度采样数据，势必会造成短周期信号的缺失，在建立热传输模型时，不存在边界条件的高阶谐波分量，进一步会导致模拟结果较大的误差的存在.

2.3 热传导对流法

Gao等(2003)在热传导对流解析解的基础上进一步得出了考虑对流作用的热扩散系数表达式为

其中φ1、φ2为别为两层温度序列中主要谐波分量的位相.Gao等(2008)分三种情况：W=0、W>0、W0与W 2.4 由热传输方程的解析解反演参数法

参数反演法中最经典的是由传统谐波法(HM)的解析表达式利用最小二乘法拟合(1.3)式中的κ，具体思路是先自取κ的初值，带入到(1.3)式中计算T，使得观测的温度序列T与计算得到T的值之差最小的κ即为所求.此法被称为求解热扩散系数的谐波法，在利用变温层观测的温度序列求解大地热流或海、湖底沉积物热流时，热扩散率的确定(Wang and Beck， 1987；Kinoshita et al.， 1996；Hamamoto et al.， 2005；Liu et al.， 2013)大多采用此方法.与此法类似的还有利用最小二乘法拟合CLTM法(Balabanis，1987)解析表达式中的κ，相同方法还可用于对双层热传导模型解析式中对κ的反演(魏东平等，1992).

Horton等(1983)用浅地表(不深于10 cm)温度序列数据将求解热扩散系数的振幅法、位相法、反正切法、对数法与谐波法进行定量比较，此后刘树华等(1991)又采用了四种不同的实测土壤温度数据比较分析了每种热扩散系数方法的特点.Verhoef等(1996)，莫兴国等(2002)、Wang等(2010)、缪育聪等(2012)相继用不同类型土壤将以上大部分求解土壤热扩散系数的方法进行比较分析，得出了较一致的结论：一是，用振幅法得到的热扩散率模拟土壤温度，位相有前置趋势.位相法得到的热扩散率模拟土壤温度时会系统地高估土壤温度振幅；二是，用反正切法和对数法求土壤热扩散系数时，不需要较多的观测数据，所以在缺少高密度测量的情况下，这两个方法优势较明显.但这也导致了他们计算的不准确性，也增加了计算结果对所选取时刻观测数据的敏感性，计算结果并不理想；三是，相对于传统的振幅法、位相法、反正切法及对数法，HM解析反演参数法得到的土壤热扩散系数对土壤温度的模拟效果最好，但当遇到阴天或者降水天气过程时结果会不太理想；四是，热传导-对流方法得到的土壤热扩散系数对夜间土壤温度模拟效果不太理想，但对白天的模拟效果很好.

3 土壤体积热容量

土壤热容量分为质量热容量和体积热容量，在研究浅层地表热传输过程中，我们主要关注的是体积热容量.土壤中固、液、气三项组成成分的体积热容量差别很大，为了应用方便， de Vries(1963)建议将土壤矿物质和有机质的体积热容量定为1.9×106 J/(m3·K)和2.5×106 J/(m3·K)，水和空气的体积热容量分别为4.2×106 J/(m3·K)和0.001×106 J/(m3·K)，空气的体积热容量很小，在计算时可忽略，所以由组分按体积比例组成的整体土壤热容量计算公式可表示为

其中，Cgm、Cgo、Cgw分别为土壤矿物质、有机质及水的体积热容量，Xm、Xo、Xw为矿物质、有机质和水分的体积组成比例.土壤水分一般由土壤湿度测量仪插入待测土壤中直接测得，此外还可以采集土壤标本后称重，烘干后再称重得到.土壤有机质的测量一般采用将烘干后的土壤标本磨成粉后高温煅烧，捕捉产生的CO2含量来得到.土壤中空气的组成比例不好获取，一般用饱和含水量减去含水量得到.水的体积热容量比其他两个组分的大，对于给定的土壤，当固体颗粒成分保持不变时，土壤容重的大小主要取决于土壤中水分的含量，即土壤含水量.对于标准采样的土壤样本，当缺少土壤饱和含水量的测量时，一般选取标本中土壤最大含水量为饱和含水量.这一处理方法会低估土壤中空气组分含量的大小，进而高估土壤体积热容量的值.

由于土壤含水量对土壤的容积热容量影响很大，Garratt(1992)提出了与土壤含水量有关的土壤体积热容量表达式为

其中，Cgs是干土(包括矿物质和有机质)的体积热容量，θ是土壤含水量，θs是饱和土壤含水量.其中假设干土体积热容量为Cgs=2.08×106 J/(m3·K).在研究浅层地表热传输时，上面两个公式是大量文献中最常见的求解土壤体积热容量的方法.

4 热导率

对土壤热导率的研究多集中于实验测量技术的开发(余正，1986；任图生等，2004a、b；Ochsner et al.， 2001)及根据土壤质地的参数化方法研究.这些研究是对热导率的直接获取，其间接获取可根据公式λ=Cgκ，通过对土壤容积热容量及热扩散系数的求解或测量得到热导率(Wang and Beck， 1987；汤懋苍等，1991；魏东平等，1992；Kinoshita et al.， 1996；Hamamoto et al.， 2005；Liu et al.， 2013).由于土壤热导率的参数化方法有着比较广泛的应用，此处我们根据提出的时间先后顺序对热导率的参数化方法进行介绍.

关于土壤热导率计算的参数化方案中的热导率几乎都是土壤质地的函数，通常根据直接测定值将公式中的经验参数不断改进，使得估计值能够更加精确地拟合观测值.被称为经典理论模型的土壤热导率计算公式(见公式(4.1))由de Vries(1963)提出.

该公式将热导率看作是土壤各组成成份的组合函数，其中fi为倍增因子，它由第i土壤组份的形状、接触面及热导率决定，Xi为第i组份所占的体积比例额，λi为第i组份的热导率.在实际应用中，Ochsner等(2001)又通过界定土壤固体颗粒、空气、水的几何形状因子，及土壤孔隙中水分和空气的热导率，并结合临界水含量的取值，对fi的取值进行了系统性研究.

Johansen等(1975)结合Kersten数(Kersten，1949)，将完全干燥及水分完全饱两种情况下土壤热导率的组合形式表达了热导率经验公式为

其中，Ke是Kerste数，λdry为完全干燥的土壤为热导率(Côté and Konrad，2005)，λsat为水分完全饱和状态下的土壤热导率.λdry取决于固体颗粒的形状和作用的物质参数.此后许多学者相继利用土壤热导率的测定值对(4.2)式的参数进行了修订与完善，其中最有代表意义的是Sundberg(1988)、Tarnawski和Leong(2000)提出的自相融逼近法，其热导率的表述为

式中，Sr为土壤湿润度(=实际含水量/饱和含水量)，λa是空气的热导率，ε是土壤孔隙度，b为热接触阻抗系数.

Camillo和Schmugge(1983)，根据土壤孔隙度及含水量构建了一个土壤热导率的经验公式为

https://www.trust-web.cn

该公式是简单生物圈模式SiB2系统强迫-恢复方法模拟地表温度中热导率的估算公式.

Campbell(1985)提出了另外一种较受大家关注的经验公式为

其中A、B、C、D、E这五个参数与石英、其他矿物、固体颗粒的总体积含量及粘土成分的体积含量等有关.

Becker等(1992、1997)通过收集大量前人观测到的土壤热导率数据，通过拟合逼近的方法得出了一种新的热导率经验公式为

其中a1、a2、a3、a4按照冻结与非冻结状态下的不同土壤质地(如：砂土、粘土、泥炭土、粉质土及砾石土)归纳出的不同参数.

Zhang等(2012)分别将以上几种经验公式运用到SiB2模式热导率的计算中，并分别对稀疏短草、季节性草甸和云杉及水稻作物覆盖的下垫面温度进行模拟，发现不同下垫面对以上热导率计算方法的敏感程度各不相同，但总体上看， de Vries(1963)、Johansen(1975)、Sundberg(1988)的算法模拟效果优于其他算法.

5 热通量

早期土壤热通量的计算方法有：(1)零值校准法(Kimball and Jackson， 1975；Pikul and Allmaras， 1984)，此方法可由20 cm深度层以上的土壤温度廓线与湿度观测资料先得到存在温度梯度为零时刻温度廓线上的热通量，再计算不存在温度梯度为零时刻的值；(2)地温曲线图解法(陆渝蓉和高国栋，1987)，用两个月之间的气温差，以及不同深度土壤温度差的相关关系式求得土壤热通量；(3)土壤热通量的参数化求解方法：地表土壤热通量是地表能量平衡系统中净辐射的线性函数(Idso et al.， 1975；Fuchs，1987；Santanello and Friedl， 2003)；地表土壤热通量是地表感热的函数(Cellier et al.， 1996).Liebethal and Foken(2007)利用时间跨度是一天的辐射及感热数据对土壤热通量进行参数化拟合，得到了较满意的拟合结果.

以上方法是在土壤观测资料相对较缺乏时提出方法和方案.一般情况下，地表土壤热通量由zr深度处的热通量与zr以上土壤的蓄热能的和组成(Foken，2008)：

在许多土壤热通量的研究工作中，大家常把上式的第二项忽略.Ochsner等(2006)在裸土、大豆冠层及玉米冠层覆盖的浅层土壤测量土壤蓄热能，认为zr的范围处在5~10 cm之间时，计算地表土壤热通量时可忽略zr以上土壤蓄热能的影响.所以地表土壤热通量求解的主要区别在于对zr深度处的热通量，即(5.1)右边第一项的求解，此项除了可用热通量板测得外，还可以用观测温度数据有限差分获得温度梯度(Liu et al.， 2013)，也可通过不同传热模型所得的温度预报方程，对其在深度上求微分，而直接得G(z，t)的解析表达式(Wang and Bras， 1999；Heusinkveld et al.， 2004；缪育聪等，2012).

通过(5.1)式求地表土壤热通量的方法延续了四十年之久，Gao(2005)在(1.13)式的基础上提出了考虑传导-对流过程的地表土壤热通量求解方法：

Gao(2005)在热传导对流方法基础上利用1998年GAME/Tibet实验那曲站数据，计算土壤热扩散系数进而计算土壤热通量，将计算的热通量运用到能量平衡系统中，发现能量平衡系数由以前的0.7改善为0.9.

6 讨论及展望

综上所述，浅层地表热传输方面的研究经过了半个多世纪的不断完善和发展.土壤是由固、液、气三相组成的多孔介质，固体颗粒质地的粗细、湿润还是干燥，有机质含量的大小等因素都决定了土壤是个复杂的介质.对其热传输的模拟从只考虑热传导到热传导-对流耦合方程的建立，从把土壤介质看成单层发展到双层的传热模型，不断发展的热传输理论越来越与真实土壤的传热过程贴近.随着计算机技术的发展，使得各种复杂运算成为了可能，在今后的工作中可以考虑建立耦合热传导-对流的多层传热模型，上边界条件可尝试先从定常温度的基础上叠加一个谐波到一组谐波，且采用各层交界面满足热性质相同的边界条件来模拟土壤的传热过程.

近些年来提出的热导率参数化方案及土壤体积热容量计算方法都是以表层土壤为研究对象发展而来的，所以这些算法非常适合于对表层土壤的计算.但对于较深层土壤或岩石，如几米到十几米深度，这些算法的适用性是需要质疑的，而在利用变温层中的温度序列数据尝试获取大地热流时，正是需要对较深层土壤或岩石的热性质有个较精准的把握.参数化方案是在大量实验结果的基础上得到的，对深层土壤进行实验的难度较浅层土壤要大很多.所以，对较深层土壤或岩石热性质的准确获取，一方面，需要大量的实验来积累深层不同质地、不同湿度土壤或不同种类岩石的实验数据，另一方面，也可转换角度，从开发与真实的深层土壤或岩石传热过程更贴切的模型入手，通过模型模拟深层热物性参数来拟补其实验数据上的不足.

致 谢 高志球教授对本文的完成提供了大量有益的帮助.王琳琳与张晓惠对本文的写作提出了有益的建议.审稿专家对本文初稿给出的很好的意见和建议，这里一并致谢.